A Gentle Intro to Complexity Theory

The primary goal of complexity theory is to understand the difficulty of computational problems. In this section, we aim to refine that statement by answering the following questions: what are some reasonable definitions of computational difficulty? And how can we effectively group problems together so that they may be studied as a collective? This section is intended to be a primer in complexity theory for those coming from a machine learning background and can safely be skipped.

We are obligated to begin with a particularly famous example: the $\text{P}$ vs. $\text{NP}$ problem. The Clay Mathematics Institute is currently offering a $1 million prize to the person who is able to crack it (definitely one of the harder ways to make a million dollars). The problem is, at a philosophical level, about how the difficulty of verifying a correct solution compares to the difficulty of computing a correct solution. The prevailing view is that the latter is strictly harder, and much of modern cryptography rests on related hardness assumptions.

Figure 1: P = NP? (barely legible) on the wall of the Princeton CS building[8].

Let's illustrate the problem with an example. Suppose that you are given a set of integers $p_1,\ldots,p_k$ which are purported to be the prime factorization of $x$. You are skeptical and would like to check this claim for yourself. Fortunately, you can do this quite easily: first verify that each $p_i$ is prime (there is a deterministic polynomial-time algorithm for this due to Agrawal et al.[1]) and then multiply the $p_i$ together to make sure that their product is $x$. This verification algorithm runs in time polynomial in the length of the input $\langle x, p_1,...,p_k \rangle$.

But what if you wanted to find the prime factorization of $x$ yourself (i.e., compute a solution)? Could you do so for an arbitrary $x$, without simply using naive trial division up to $\lfloor \sqrt{x} \rfloor$ (which takes time exponential in the input length $|x| = \lceil \log_2 x \rceil$)? If indeed there were an efficient algorithm for this problem, it would break RSA-style cryptosystems, but notably its existence would not resolve the $\text{P}$ vs. $\text{NP}$ problem¹.

Now for a more precise definition: $\text{P}$ is the class of decision problems that admit a polynomial-time (polytime) solution. More concretely, a language $L \subseteq \{0, 1\}^*$ is in $\text{P}$ if there exists a deterministic algorithm $A$ and a polynomial $q$ such that on each input $x$, $A$ halts within $q(|x|)$ steps and $A(x) = 1$ if and only if $x \in L$. Here "language" refers to the set of yes-instances for a particular decision problem. As an example, the following language defines a decision version of integer factoring

$L_{\text{factor}} := \{\langle x, p_1,...,p_{k} \rangle \mid \text{ each } p_i \text{ is prime and } \prod_{i=1}^k p_i = x\}$.

A problem is in the class $\text{NP}$ if and only if it admits a verifier that, given an input and a proposed solution, checks correctness in polytime. Earlier, we exhibited such a verifier for a decision version of integer factoring. In that case, the proposed solution consisted of the input $x$ together with integers $p_1,\ldots,p_k$ claimed to factor
$x$; this extra piece is called a certificate (or witness) and is required to have length polynomial in $\lvert x\rvert$. The $\mathrm{P}$ vs. $\mathrm{NP}$ problem asks whether every problem with efficiently verifiable certificates can also be solved efficiently—i.e., whether $\mathrm{P}$ and $\mathrm{NP}$ are actually the same set.

We have seen two different ways of grouping infinite sets of problems, and in both cases, we used time complexity as a measure of difficulty. Other measures of difficulty include space complexity and bits of communication, and there is a whole zoology of problem classes that result from these[6]. Another interesting example is the class $\text{IP}$ which is the set of problems that can be solved by a polytime randomized verifier interacting with a (potentially adversarial) computationally unbounded machine. It turns out that $\text{IP}$ exactly captures the problems that can be solved with polynomial space[2].

Short Circuit

The $\text{P}$ vs. $\text{NP}$ problem concerns the limits of efficient computation on Turing machines which is the model that best captures the capabilities of classical computers (the Church-Turing thesis posits that Turing machines exactly capture the power of computers). We will now switch from Turing machines to circuits, which will generate a classification scheme that is more useful for studying transformers.

A (Boolean) circuit is a finite DAG with Boolean gates (i.e., NOT, AND, and OR). Let's assume that we would like to use circuits to solve decision problems; in particular, we will consider circuits that have just one output gate. The architecture of a circuit, including the number of input gates it has, is not allowed to change according to its input so a separate circuit is required for each input length. Thus, to solve a decision problem $A$ on all input lengths, we will need an infinite family of circuits, $\{C_n\}_{n=1}^{\infty}$, where $C_n$ computes $A$ on inputs of length $n$. In this sense, circuits are non-uniform: the circuits $\{C_n\}$ may have different structures and it may even be the case that there is no single finite algorithm that can generate them all. This is in contrast to Turing machines, which have a single finite description used for all inputs.

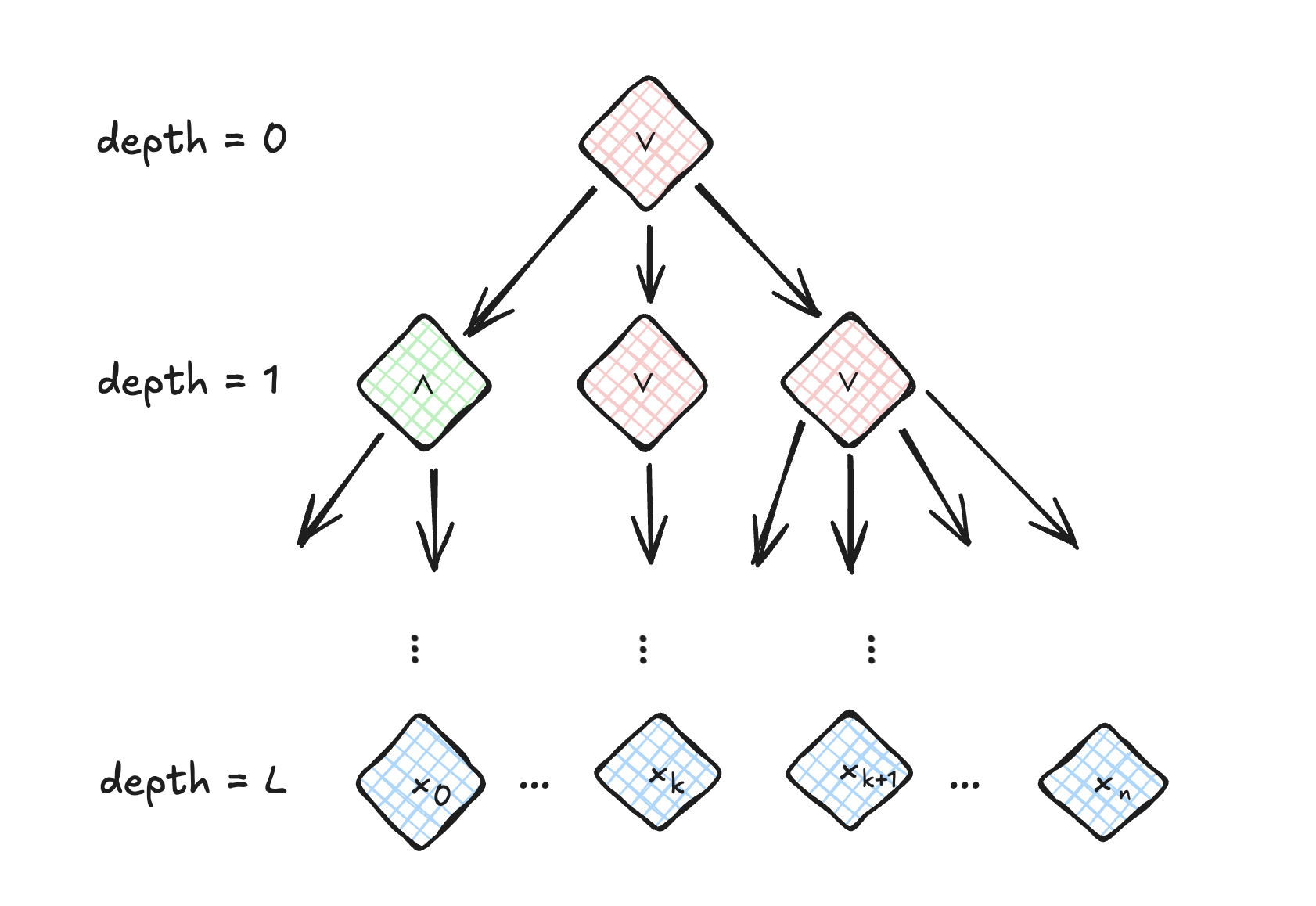Figure 2: A simple circuit, with depth $L$, a single output gate, and $n$ input gates.

One way to measure the difficulty of a problem is by the size of the smallest circuit family that can solve it. More concretely, $A \in \text{SIZE}(K(n))$ if there exists a family of circuits $\{C_n\}_{n=1}^\infty$ such that for all $n$, and for each $x$ with $|x| = n$, we have $A(x) = C_n(x)$ and $C_n$ has at most $K(n)$ gates. The set of problems that can be solved by circuits with polynomially many gates is called $\text{P/poly}$ and one can show that $\text{P} \subseteq \text{P/poly}$. So in particular, if $\text{NP} \not\subseteq \text{P/poly}$ then $\text{P} \neq \text{NP}$. That is, if $\text{NP}$ requires superpolynomial-sized circuits then $\text{P} \neq \text{NP}$.

The depth of a circuit is the length of the longest path from the output node to any input node. We can think of depth as measuring the extent to which a computation can be parallelized. For example, the circuit in Figure 2 has $L$ levels (where each level is the set of nodes with the same distance from the output layer). The nodes in level $r$ depend on the computation done in levels $r+1,\ldots,L$ which determines the inputs to the layer. However within a layer, there is no interdependence between nodes. Thus, problems that can be solved by circuits of low depth are more parallelizable. We will use these complexity metrics—size and depth—to define the class $\text{AC}^0$, which will come up in our discussion of transformers.

Definition. $\text{AC}^0$ is the class of problems that are computable by circuits with polynomial size and constant depth. Additionally, nodes are allowed to have unbounded fan-in.

Optimus Prime

Transformers are not circuits, nor are they Turing machines. The method by which transformers compute answers to problems is fundamentally different from either of these other models of computation. Hao et al. formally define a (restricted) model of computation for transformers called $\text{AHAT}[\mathbb{D}]$ where $\mathbb{D}$ is the data type on which the transformers operate[7]. We will define the high-level features of this class when we discuss a fundamental result in transformer complexity which helped to spur current research in the area. For the remainder of the article, we will use $\mathbb{F}$ to denote the set of floating-point numbers with $O(\log n)$ bits of precision.

Definition (Saturated Attention). For attention scores $a \in \mathbb{F}^n$, let $\mathcal{M}(a) := \{i | a_i = \max_j a_j\}$ be the set of indices attaining the maximum. Note that if $a$ has a unique largest entry, then $\mathcal{M}(a)$ will be a singleton. We define the saturated attention of $a$ as

$\zeta(a)_j = \frac{1}{|\mathcal{M}(a)|} \cdot \begin{cases} 1 & \text{if } j \in \mathcal{M}(a) \\ 0 & \text{otherwise} \end{cases}$

Intuitively, $\zeta$ defines a discrete uniform distribution over maxima. Observe that saturated attention is the zero-temperature limit of traditional softmax attention,

$\lim_{\tau \to 0} \text{softmax}(a/\tau) = \zeta(a)$

Vanilla softmax attention heads often learn diffuse distributions over tokens, making this model of attention fairly unrealistic. However, we can use this simplified model to prove a theorem on the expressivity of transformers. First, we need to define what it means for a so-called saturated transformer to recognize a language: a saturated transformer $M \in \text{AHAT}[\mathbb{F}]$ recognizes a language $L$ if there exists an affine linear transformation $(W, b)$ such that $W \cdot M(x) + b > 0$ if and only if $x \in L$. In particular, $(W, b)$ separates positive examples from negative ones using the $x$-axis. We will refer to $(W, b)$ as an attention readout.

Theorem (Merrill et al. [3]). Saturated transformers with $O(\log n)$ bits of floating-point precision can compute problems outside of $\text{AC}^0$.

Proof outline: Let $\text{MAJ} := \{w \in \{0, 1\}^* : w \text{ has strictly more 1s than 0s}\}$

Since $\text{MAJ} \notin \text{AC}^0$ it suffices to show that saturated transformers can recognize $\text{MAJ}$. We can do this with a 1-layer, 1-head transformer. These are its components:

• Positional embedding: Let $\phi : \{0, 1\} \times \mathbb{N} \to \mathbb{F}^{2n}$ be a one-hot encoding ². In particular, for a sequence $w = w_1w_2\ldots w_n$, the $i$-th token is encoded as:

Let $x_i = \phi(w_i, i)$ denote the $i$-th token after applying positional encoding, and let $X \in \mathbb{F}^{n \times 2n}$ be the matrix of these encodings $X = [x_1; x_2; \ldots; x_n]$.

• Attention scores: the score function $s : \mathbb{F}^{2n} \times \mathbb{F}^{2n} \to \mathbb{F}$ is constant at 1. That is, for each $i, j \in [n]$, $s(x_i, x_j) = 1$, so attention is uniform over all tokens. Note that we are constructing a transformer with a single head and a single layer, so there is only one score function to specify.
• Post attention: we describe a single function $f : \mathbb{F}^{2n} \times \mathbb{F}^{2n} \to \mathbb{F}^{2n}$ that computes the post attention layer, per-position update. In a vanilla transformer, $f$ would apply the FFN, residual connection and layer norm(s). We use $f(a, b) = b$.
• Attention readout: Let $W=[-\mathbf{1}_n^\intercal\ \ \mathbf{1}_n^\intercal] \in \mathbb{F}^{1 \times 2n}$ and $b=0$ where $\mathbf{1}_n^\intercal$ denotes a row vector of all 1s.

Let $a_i \in \mathbb{F}^n$ be the attention score vector defined as $(a_i)_j = s(x_i, x_j) = 1$. Observe that $\zeta(a_i) = (1/n, 1/n, \dots, 1/n)$ for each $i$ and

$\zeta(a_i)^T X = \frac{1}{n}\left( \mathbf{1}\{w_1 = 0\}, \dots,\mathbf{1}\{w_n = 0\},\mathbf{1}\{w_1 = 1\},\dots,\mathbf{1}\{w_n = 1\}\right)$

Let $z_i = \zeta(a_i)^T X$. Finally, since $f(x_i, z_i) = z_i$ we have

$W\cdot f(x_i, z_i)+b = \frac{1}{n}\left( \sum_{j=1}^{n} \mathbf{1}\{w_j = 1\}-\sum_{j=1}^{n} \mathbf{1}\{w_j = 0\} \right)$

This quantity is greater than zero exactly when there are more 1s than 0s in $w$. Hence, this transformer recognizes $\mathrm{MAJ}$. $\square$

Merrill et al. go on to show that floating-point saturated transformers can be simulated by threshold circuits, giving an upper bound on their expressivity. Briefly, threshold circuits are allowed to use gates that activate when the number of input 1s is above or below a certain fixed threshold. The class of problems that can be solved by threshold circuits of constant depth is called $\text{TC}^0$, so formally, the containment result is $\text{AHAT}[\mathbb{F}] \subseteq \text{TC}^0$.

Takeaways

We showed how tools from complexity theory can be used to analyze a restricted transformer model called floating-point saturated transformers, and we contextualized the expressivity of this model using Boolean circuit classes. This kind of classification has proven to be useful both in motivating new architectures and understanding the fundamental limitations of current ones.

We allowed saturated transformers the freedom of using $O(\log n)$ bits of floating-point precision, which we used when defining the positional embedding function $\phi$. Intuitively, this assumption bounded the memory of our transformer model to be $O(n \log n)$ (each of the $n$ input tokens uses $O(\log n)$ bits). This amount of memory sufficed for representing token indices and counts up to $n$, ensuring the saturated-attention construction was well-defined. In practical settings, there will be a fixed maximum context window length $N$; choosing a fixed float type with mantissa at least $\log N$ bits will then recover the same behavior.

Merrill & Sabharwal extended the containment result $\text{AHAT}[\mathbb{F}] \subseteq \text{TC}^0$ to softmax-attention transformers, showing that they can also be simulated by $\text{TC}^0$ circuits[4]. Behrouz et al. find that Titans can compute problems outside of $\text{TC}^0$, making them theoretically more expressive than both softmax-attention transformers and other test-time learners like DeltaNet[5]. As a future direction, we are interested in studying the gap between a transformer’s theoretical expressivity and what it can actually learn in realistic training settings. In other words, given a function that a transformer is capable of representing, can practical training setups (objective, optimizer, data, precision/compute) reliably recover it?