Back
Sparsity is Cool
Summary
- Sparse attention models have recently emerged as strong competitors to base attention.
- These methods are much faster, and natively-trainable variants such as NSA even outcompete on expressivity.
- We report preliminary investigations into the attention landscape of sparse attention models.
- We present the first attention maps at long context, as well as a deep dive into attention sinks and key geometry.
- We propose and evaluate further inference-time improvements on NSA motivated by mechanistic analysis, demonstrating minimal performance degradation.
- A new hardware-aware Triton-based NSA kernel implementation for high throughput training and evaluation of sparse attention.
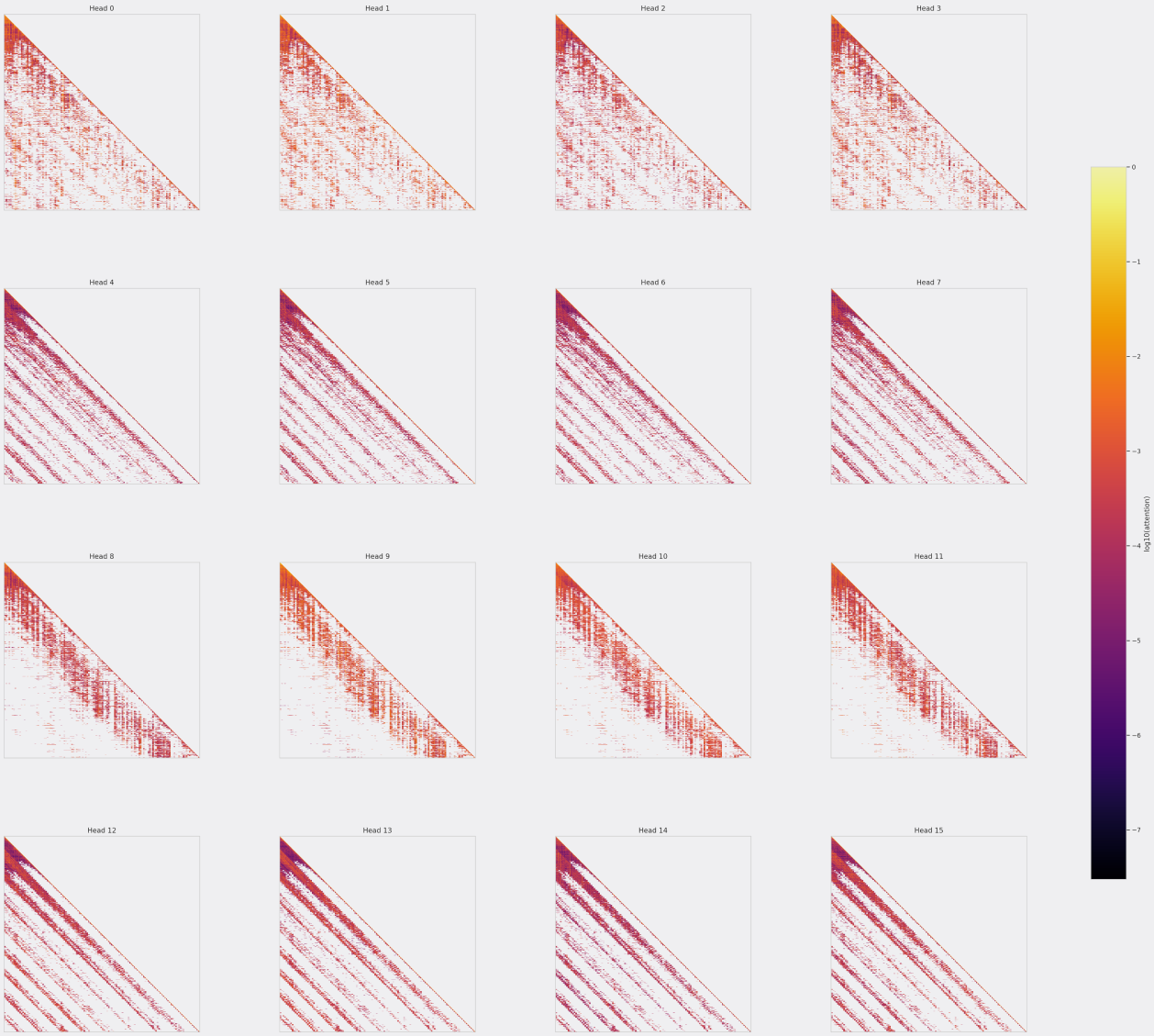 NSA's selection branch learns to focus on various subsets of tokens, reducing the computational cost of attention.
NSA's selection branch learns to focus on various subsets of tokens, reducing the computational cost of attention.
Introduction
Today, nearly all large language models (LLMs) are built on the transformer architecture. However, due to the self-attention mechanism, scaling transformers to longer contexts can be difficult: attention requires computing dot products between every query and every key, hence the computation scales quadratically with sequence length.
But the assumption that every token needs to attend to every other token is rarely justified. In practice, attention distributions are highly sparse: most queries place significant weight on only a small subset of keys. Thus, for both training efficiency and inference-time speedup reasons, it is natural to try to build sparsity directly **into the architecture. There have been many previous attempts [1][2][3] to do this, but most fall short in one of two ways. First, many approaches apply sparsity only at inference time, missing out on training-time efficiency and often degrading performance, since the model must suddenly operate under activation patterns it was never optimized for. Second, even when sparsity is applied during training, the implementation is often not hardware-aligned, e.g. relies on non-contiguous memory access, or utilizes non-differentiable operations like clustering which weaken the model's ability to learn effectively.
This motivates hardware-aligned, natively-trainable forms of sparse attention. Two recent approaches are Moonshot AI's Mixture of Block Attention (MoBA) and DeepSeek AI's Native Sparse Attention (NSA) [4] [5]. These methods significantly outperform inference time-only interventions while being much faster than base attention, especially at long contexts.
The main idea of MoBA is to subdivide the context length into blocks, and then route the current query token into the K blocks with the highest affinity score (in addition to the current block). The standard attention operation is replaced with , where I represents the selected block indices.
These affinity scores are calculated in a parameter-free way: they are given by the inner product of q and the mean pooling of K[I_i] along the sequence dimension. While this is quite nice from an efficiency point of view, it (likely) prevents optimal routing.
Given a context length of 8192, the authors choose the MoBA hyperparameter as block size 512 and TopK of 3, which creates 80% sparsity. They find that this is quite competitive with full attention.
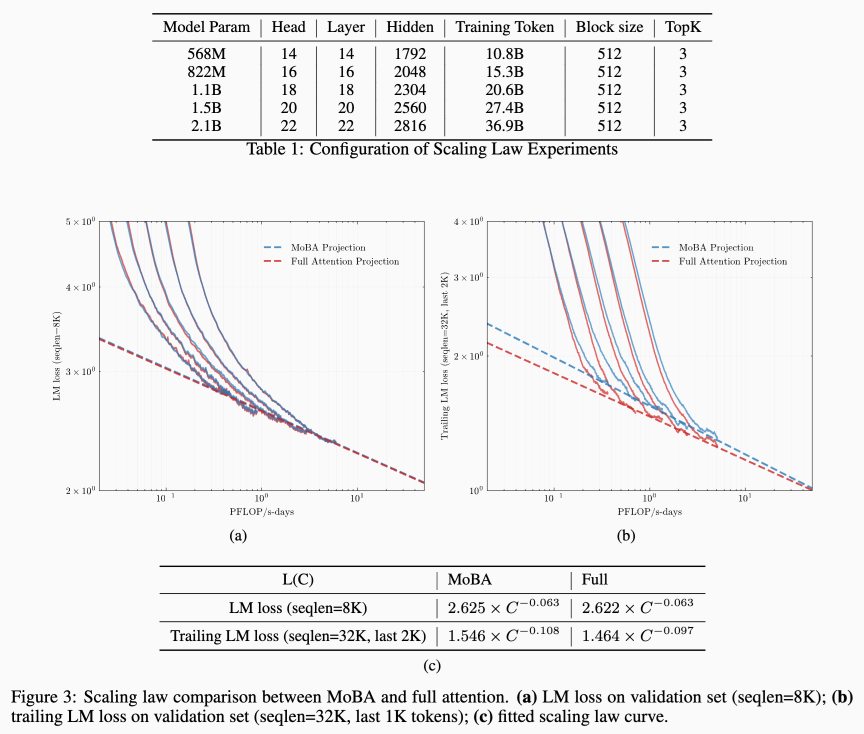 Loss curves for MoBA [4].
Loss curves for MoBA [4].
NSA on the other hand utilizes a multi-branch architecture where each query token computes attention over three separate contexts: compressed, selected, and local, and then blends their outputs with a learned gate. Mathematically, this is given by
where the gate scores are dynamically predicted by an MLP with a sigmoid output.
The compression branch subdivides the previous keys (resp. values) into (typically overlapping) blocks, and then an MLP with intra-block positional encodings is applied to produce a compressed key (resp. value) for each block. NSA then performs compressed attention between the queries and the compressed keys/values.
The selection branch uses the attention scores computed in the compression branch as "importance scores", and then does full attention on the concatenation of the blocks with the TopK importance scores (note: this is only true when compression blocks and selection blocks share the same blocking scheme. To see the calculation in general, see the NSA paper)
The window branch is standard sliding window attention: full attention on the most recent w tokens.
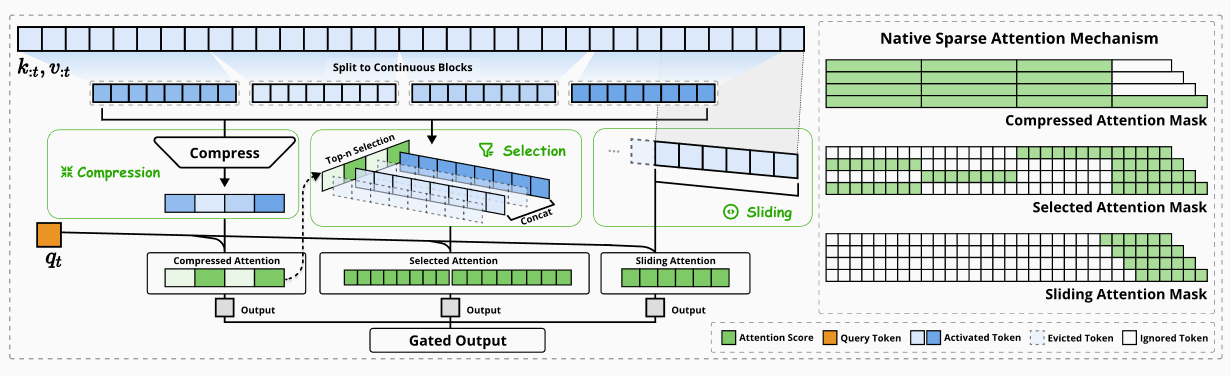 Overview of NSA's architecture showing three parallel attention branches (compressed, selected, and sliding) and their corresponding attention patterns. Green regions show where attention is computed [5].
Overview of NSA's architecture showing three parallel attention branches (compressed, selected, and sliding) and their corresponding attention patterns. Green regions show where attention is computed [5].
A particularly nice feature of NSA is that each part of the process is connected to the computation graph (i.e. is trainable). DeepSeek finds that NSA outperforms full attention performance-wise on a range of benchmarks, and from an efficiency point of view, offers significant speedups compared to FlashAttention-2: a 9x forward-time speedup and a 6x backward-time speedup.
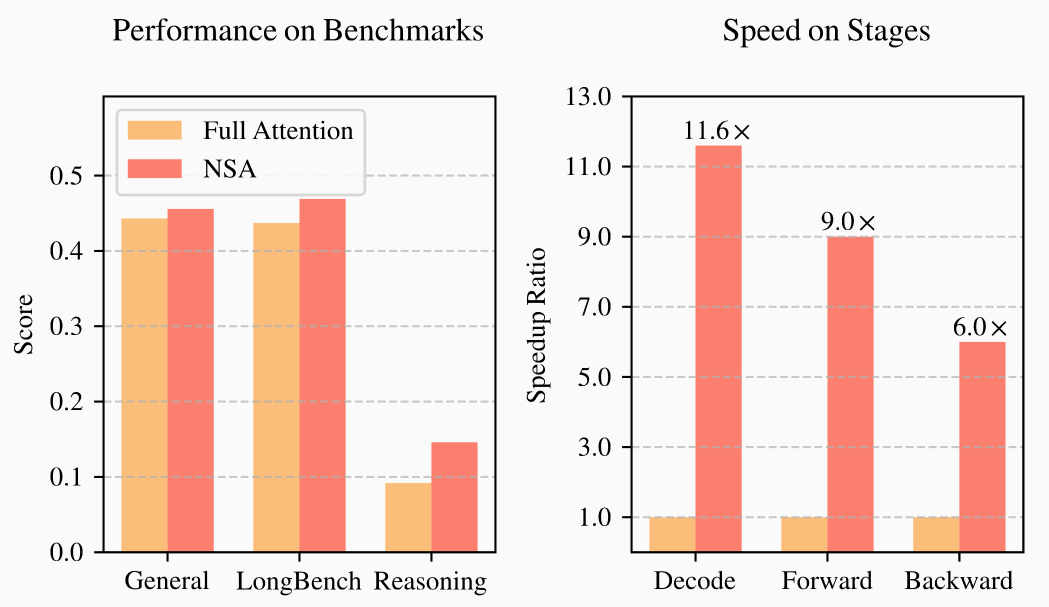
For further details on motivating sparse attention, please consult Appendix B.
Methods
Training
For our experiments, we pretrained small language models using the torchtitan library [6], with FSDP. We trained each model across four H100 nodes with Infiniband interconnects from Nebius AI. We trained models according to compute-optimal scaling laws at sizes similar to those commonly reported in the architecture research literature.
| Num params | Num training tokens | Num layers | Batch size (tokens) | Max LR |
|---|---|---|---|---|
| 340M | 15B | 24 | 0.5M | 3e-4 |
| 1.3B | 100B | 24 | 2M | 4e-4 |
For further details on our configuration and architecture, please reference Appendix A.
Hardware-Aware Implementation
Overview
We base our work off the MoBA kernel publicly released by Kimi Moonshot [4] and the NSA kernel developed by FLA-org [7]. We note that both are not fully sufficient - the former has not yet released a decode-optimized kernel for generation and the latter suffers from performance bottlenecks addressed in the hardware section.
We also test varying group sizes for sparse attention, specifically MHA, GQA (4 kv heads), and MQA for transformer and MoBA. For NSA we only test GQA (4 kv heads), and MQA. This is because hardware-aligned NSA exploits shared query groups, and MHA NSA is significantly slower than full attention or MoBA as a result (and would not be used in practice).
Our NSA implementation is publicly available at tilde-research/nsa-impl.
Hardware Challenges
As discussed before, sparse attention aims to improve attention's efficiency by reducing the number of low-importance attention computations between pairs of tokens, focusing on the most salient token interactions and effectively performing computation only on a sparse subset of pairs. However, translating this theoretical sparsity into practical performance gains presents several challenges:
Predicting sparsity patterns is costly: Dynamic sparsity incurs the overhead of computing importance or similarity matrix before determining the computation to perform. This overhead can negate the benefits of reduced computation.
Memory access patterns matter: Modern hardware is tuned to perform coalesced memory access through pre-fetching, cache hierarchies, wide memory buses and other hardware optimizations to optimize sequential memory access. Random sparse access patterns can result in poor memory bandwidth utilization.
Thankfully, attention's sparsity is not random but exhibits clear structure:
- Block-wise Patterns: As demonstrated in the NSA paper, tokens tend to attend to contiguous blocks rather than randomly scattered tokens.
- Locality Patterns: Tokens show attend strongly to other nearby tokens, motivating both MoBA's current block's attention and NSA's sliding window branch.
- Predictable Structures: This regularity enables efficient block-based selection that aligns with GPU memory hierarchy.
This key insight enables the design of efficient kernels for both MoBA and NSA.
NSA Implementation Details
Since the NSA paper did not provide a reference implementation, we implement NSA guided by the paper and leveraging the public Flash Linear Attention (FLA) repository [7]. While the NSA paper gives insights into the kernel design of a sparse attention algorithm, several critical implementation decisions determine whether theoretical speedups will translate into practice.
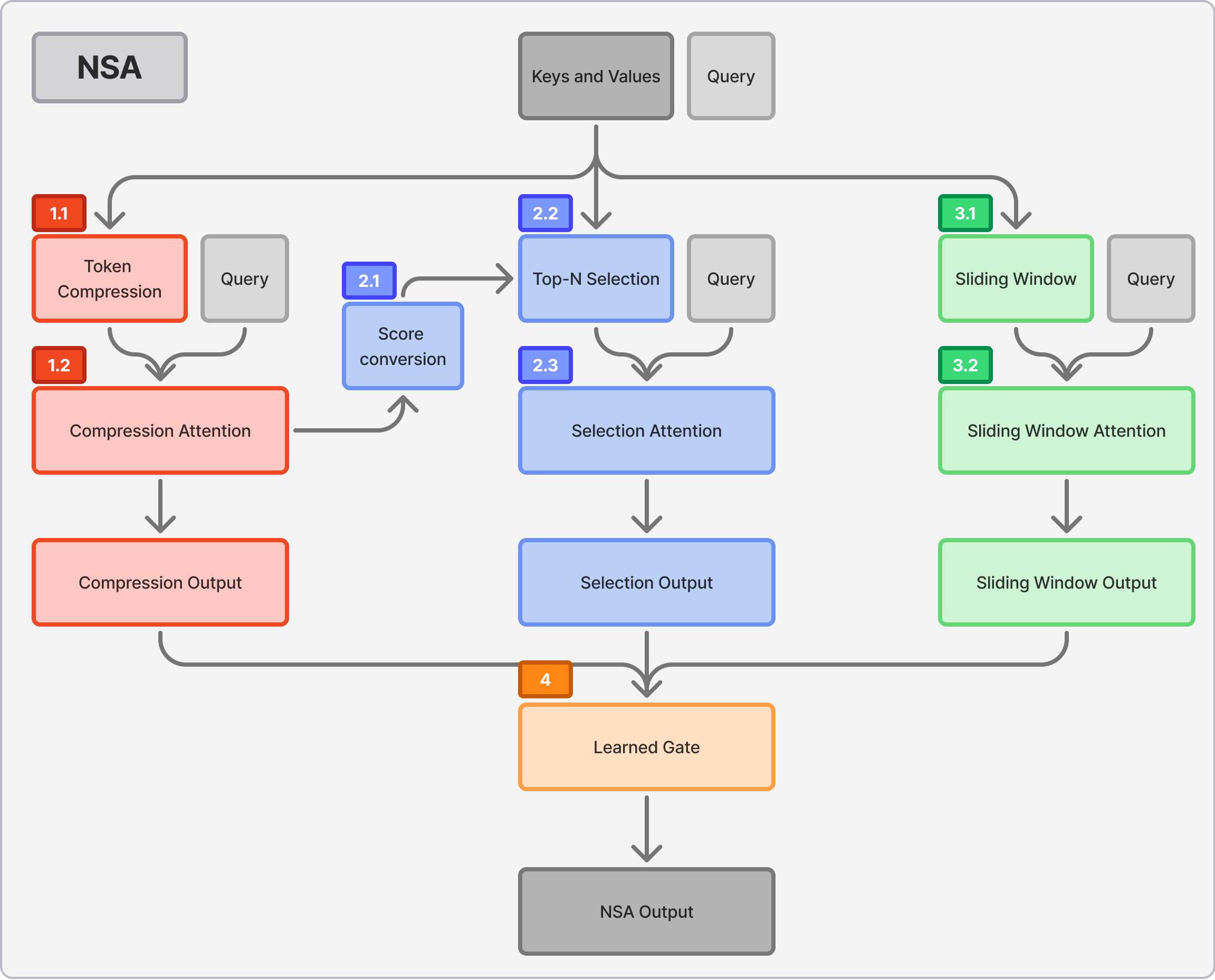 Overview diagram of our NSA implementation. The following sections detail the implementation of labeled components.
Overview diagram of our NSA implementation. The following sections detail the implementation of labeled components.
1. Compression Branch
(1.1) Partitioning & Compression (PyTorch)
Given the lack of specifics for the compression function φ in the NSA paper, our module accepts a user-defined compression function during initialization. For benchmarking and testing, we use mean-pooling as our compression function.
(1.2) Compression Attention (Flex Attention)
Compression attention follows standard attention with the original queries and the compressed keys and values. The only difference is the custom causal masking we implement via Flex Attention [8]. Specifically, for a compressed key representing tokens, we apply masking based on whether the query position precedes the first token in the corresponding block to ensure causal relationship.
2. Selection Branch
(2.1) Compute Importance Scores (Triton)
A Triton kernel recovers compression attention scores using log-sum-exponent values from the compression branch and then performs online top-k reduction to select the highest scoring blocks per query.
(2.2 & 2.3) Selection Attention (Triton)
Selection is the main architectural challenge in NSA. Each query attends to a unique subset of selected keys and values. Naively, this means explicitly unrolling and materializing different key/value subsets per query, causing inefficient memory access and poor GPU utilization.
Solution (Forward Kernel):
To avoid explicit unrolling, we implement a custom Triton kernel inspired by the NSA paper. This kernel:
- Dynamically indexes into keys/values according to the pre-computed top-N indices for each query.
- Computes scaled dot-product attention directly within the kernel.
- Uses fused operations to stabilize softmax (log-sum-exp trick).
- Stores outputs and intermediate LSE values efficiently.
Solution (Backward Kernel):
Unfortunately, the NSA paper does not provide details regarding the backward implementation. The backward implementation poses an additional challenge: Flash Attention's backward pass is key/value stationary, but NSA cannot use this approach directly since the position of each key/value depends uniquely on the query indices. We evaluate two candidate approaches:
- Single-Pass: Query-Stationary with Atomics
- Gradients are computed per query and aggregated across selected keys and values using Triton atomic operations.
- Parallelize over attention heads (following the forward pass approach).
- Minimizes memory passes but suffers overhead from atomic contentions when keys are reused across queries.
- Two-Pass: Query and Key/Value Stationary
- Reconstruct reverse mapping from key/value pairs to queries.
- In the first pass compute gradients over queries; In the second compute gradients for keys and values.
- Requires redundant computation between the two passes and more memory access but avoids atomic contention and out of order writes.
While the first approach is theoretically more efficient due to fewer passes, empirical results show that the two-pass kernel is consistently faster given our selection configuration. We adopt the second approach for all evaluation presented.
3. Sliding Window Branch
(3.1 & 3.2) Sliding Window Attention (Flash Attention)
We use the native sliding window support in FlashAttention, specifying a window size of tokens. No custom kernel or postprocessing is needed.
4. Output Combination
(4) Learned Gate (PyTorch)
For our benchmarking evaluation we use a simple two-layer MLP with Sigmoid activation to compute per-head weights. Finally, we perform a weighted sum on the outputs of the three branches.
Benchmarking Results
We evaluate NSA's performance and compare it against both dense Transformer and MoBA (FLA implementation) on a node equipped with 8 H100 GPUs. All benchmarks use MHA with 16 query blocks in BF16, and reported timings and throughput are per GPU.
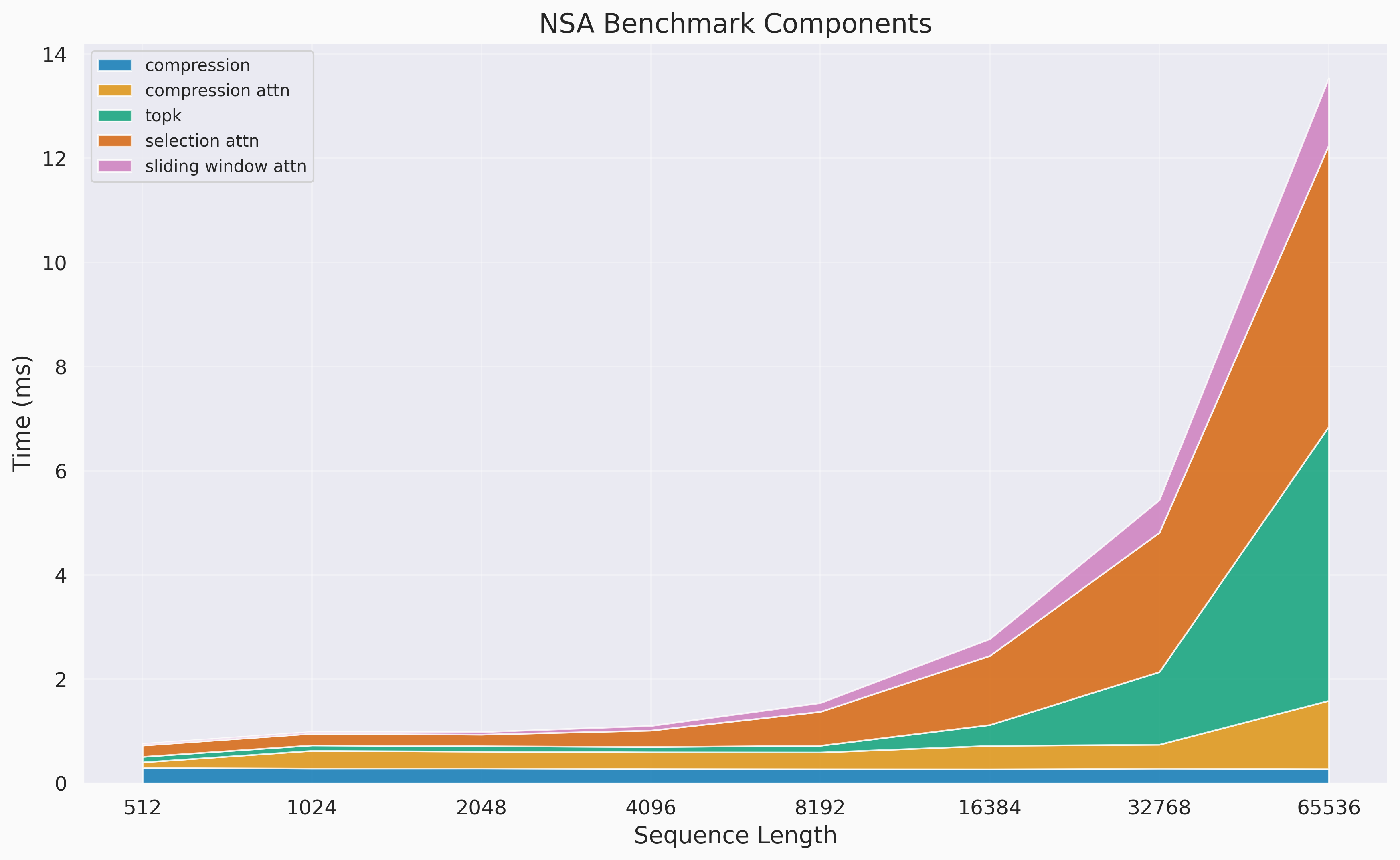 Per-GPU inference (forward) latency (ms) showing scaling of compression, compression attention, top-k, selection attention, and sliding window attention across sequence length of 512 to 65k tokens. Selection attention and the top-operation dominate latency.
Per-GPU inference (forward) latency (ms) showing scaling of compression, compression attention, top-k, selection attention, and sliding window attention across sequence length of 512 to 65k tokens. Selection attention and the top-operation dominate latency.
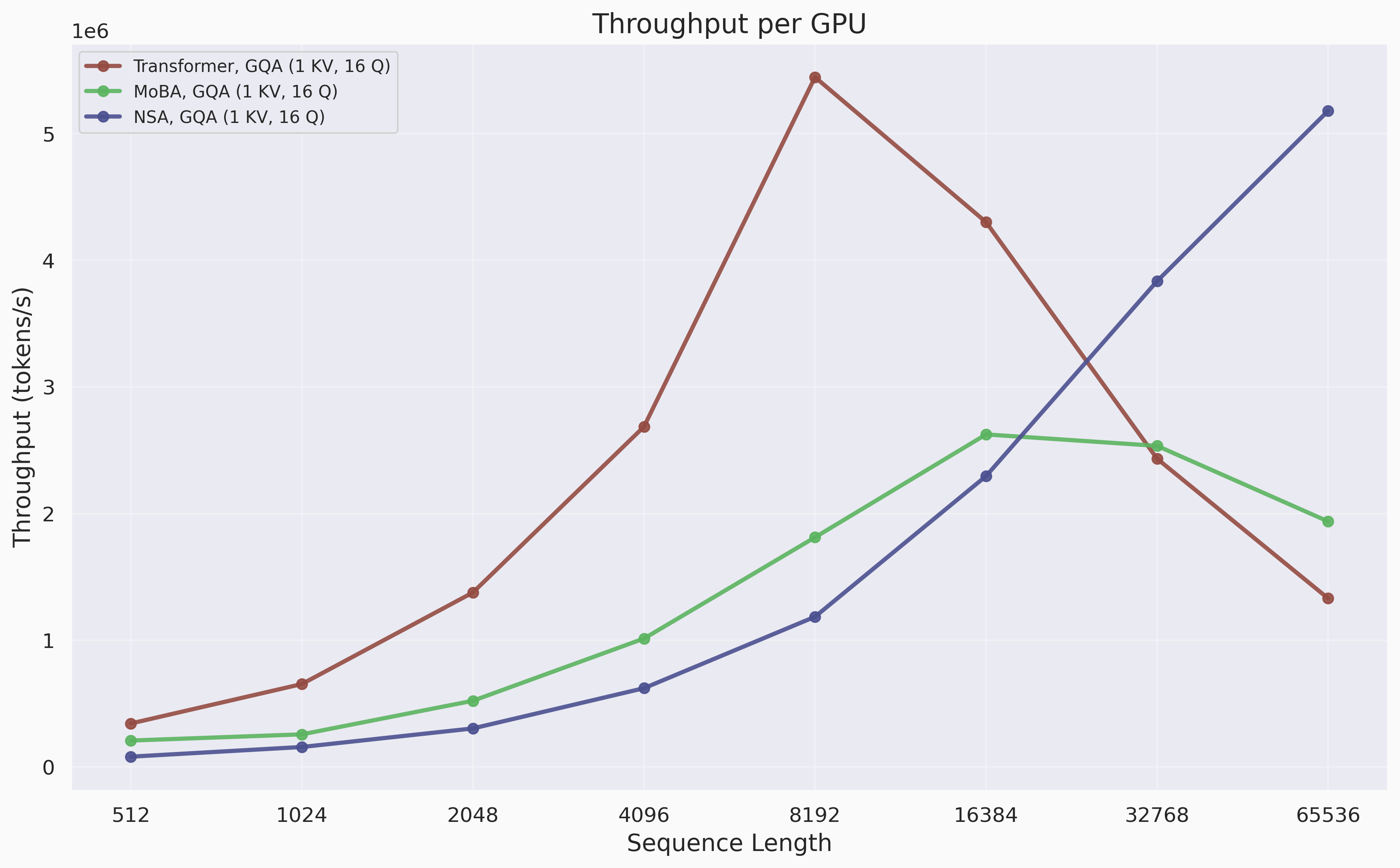 Per-GPU throughput (tokens/s) comparison across sequence length of 512 to 65k tokens.
Per-GPU throughput (tokens/s) comparison across sequence length of 512 to 65k tokens.
Evaluation
We evaluate models in two primary ways:
- Long-context perplexity evals on four datasets (CodeParrot, GovReport, PG19, NarrativeQA).
- Held-out perplexity on SlimPajama.
The models are not instruction-tuned, and thus suffer poor performance on QA-style tasks.
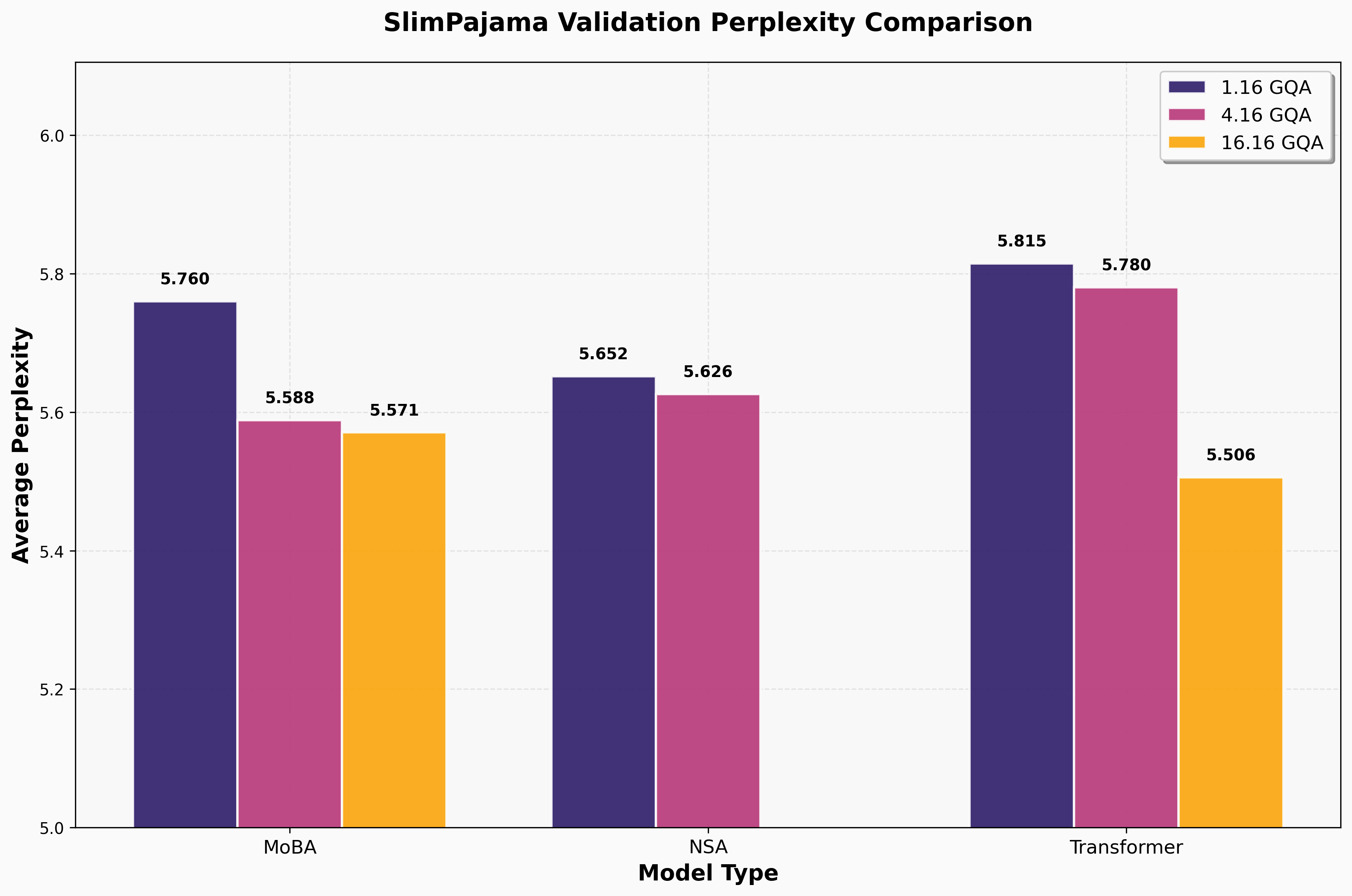 SlimPajama perplexity on held-out set. As noted earlier, we do not train the MHA NSA model as it is not kv head-parallel aligned.
SlimPajama perplexity on held-out set. As noted earlier, we do not train the MHA NSA model as it is not kv head-parallel aligned.
We reproduce NSA outcompeting dense attention in the GQA and MQA regime. Notably, MoBA also beats transformers when KV sharing is introduced. We elaborate more on potential causes for this phenomena in the key geometry section.
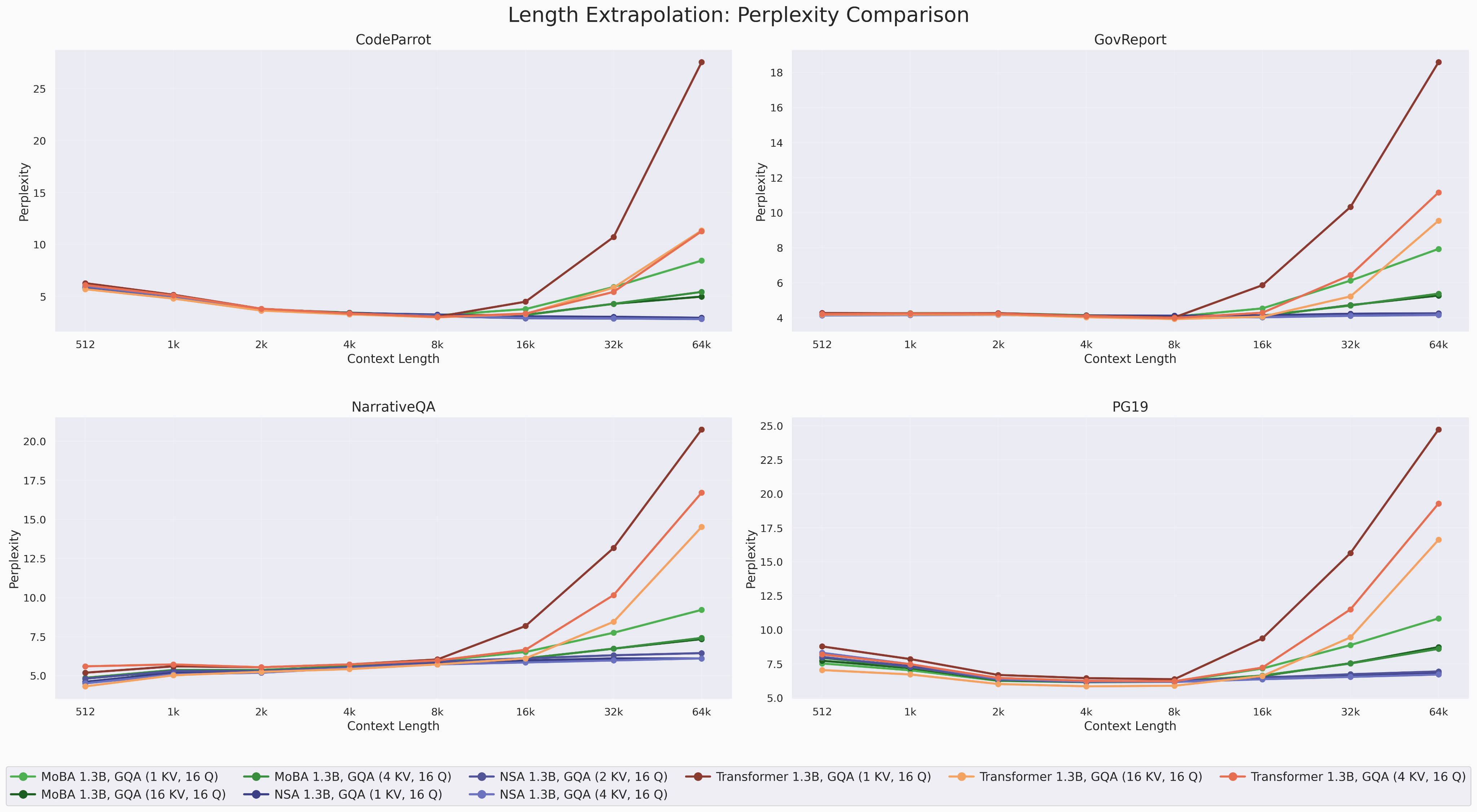 Length extrapolation results for sparse attention models.
Length extrapolation results for sparse attention models.
Sparse attention models have much stronger length generalization capabilities compared to dense attention models. NSA, in particular, sees almost no degradation over context length up to 64k.
Within an attention class, more KV heads helps with length generalization (and is generally more expressive). It is worth observing that the gain from increasing the number of KV heads is much smaller for MoBA and NSA than it is for MHA.
We also note that at short contexts, the transformer sometimes beats the two sparse attention mechanisms. This result is likely a consequence of the learned key geometry/representations as opposed to the attention mechanism itself. For sequence lengths ≤1.5k for example, NSA and MoBA are fully dense, i.e. they attend to every key.
Notably, we do not apply (dynamic) YaRN to any of the models, so length extrapolation is tested out-of-box.
Demystifying Sparse Attention Patterns
We present below the first study of sparse attention patterns at long context, as well as a characterization of their differences from full attention. The below interactive visualization displays sample attention maps for an intermediate layer of a MoBA model on an 8192 token-length sample of the GovReport dataset.
As in full attention, transformer heads specialize in different operations. We characterize four variants of MoBA heads:
- Extended SWA: Many MoBA heads clearly implement extended sliding window attention, whereby retrieved blocks are contiguous to the ongoing sliding window. This suggests a possibility for optimizing the computation in these heads by replacing them with SWA with window size 1536.
- Prefix attention: Some heads, especially at longer contexts, consistently retrieve early blocks in addition to recent sliding window. As observed in previous works such as StreamingLLM, the early block plays a crucial role in both attention sinking and initial semantic information, i.e. the prompt, and these heads function accordingly. These heads can also be compressed through SWA
- Dilated SWA: These heads are less common, but exhibit consistent checkerboard attention patterns. They are characterized by attending to blocks in a pattern resembling a dilated convolution, with regular, repeated spacing.
- Mixture: These heads are the most incompressible, they mimic dense attention patterns, with spatially contiguous queries fetching very different key/value blocks. These heads are most common in earlier layers of the model.
For NSA, the attention patterns look noticeably different. For example, selection heads often play a fixed lookback role, attending to keys/values a fixed amount in the past.
It is worth noting that the NSA model shown above was trained with GQA (4 KV heads), whereas the other two were MHA models (16 KV heads). The heavy grouping of NSA here likely leads to sparser attention patterns per head and more similar-looking maps across heads, due to shared set of keys/values. We observed models with GQA and particularly MQA had significantly different key geometry than MHA models, which we describe briefly in one of the sections below.
Attention Sinks
Attention sinks are tokens whose keys receive disproportionate attention score. Since softmax normalization forces attention scores to sum to one, in contexts where a given head may want to modulate its total contribution to be less than one, the head may align its query with an attention sink key. This allows it to soak up some portion of the normalization factor in the attention sink token, which has a characteristically small value vector, further suggestive of its role as avoiding extra computation.
Well-trained transformer language models exhibit attention sinks, with the canonical examples being the BoS token. Since the token is never used in any semantically meaningful context and is always present, the model can freely use it for sinking. As a result, studies have shown the BoS token receives very high average attention score across model families and scales, particularly for later layers of the model.
As discussed in Gu et al. [9] attention sinks display a) massive activations, b) abnormally low key vector norms and c) abnormally low value vector norms. Properties b and c can be motivated based on findings from the paper: Sinking relies on cosine similarity between query and sink keys, not magnitude, since the model wants to be able to retain most of its query-key space without having to worry about accidentally sinking. By making key magnitude low, sinking occurs only if the direction is very strongly aligned with the sink. Furthermore, when sinking occurs, the value vector for the sink should not contribute to the model residual state because the operation corresponds to a NO-OP, and as such the value norm is decreased.
By inspecting scatterplots of value norm vs attention score, we motivate a heuristic for identifying attention sinks.
We define attention sinks using the following heuristic:
where is the average attention score received by the key and is the value norm for a given token. Notably, we compute based only on the queries the immediately follow the key. We found that computing the average across all subsequent keys erased all influence of early sinks, since after some duration in context they become unused. We find this sliding average accounts for the transiency of attention sinks in practice.
Interestingly, we find that MoBA sparse attention models introduce many more attention sinks to compensate for not pulling in the first block. These attention sinks are transient and play the role within the block.
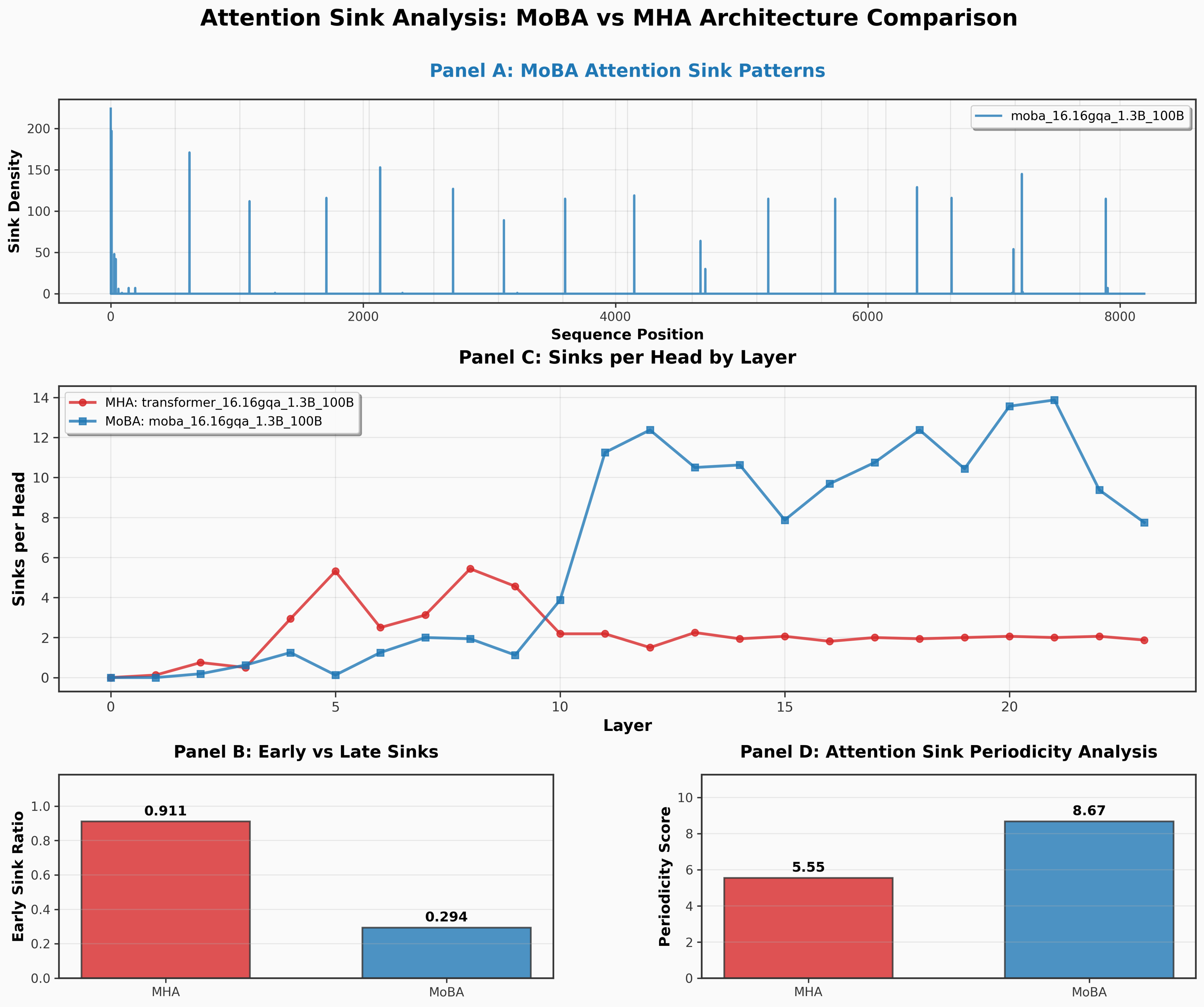 Attention sink trends for MoBA vs transformer. MoBA introduces more sinks periodically throughout the context.
Attention sink trends for MoBA vs transformer. MoBA introduces more sinks periodically throughout the context.
MoBA introduces sinks roughly at a rate proportional to its block size, indicating that it finds a sink token to live in each block. This way, regardless of which blocks are retrieved by the sparse attention mechanism, there will always be at least one sink key/value.
In NSA, the authors propose always including the first block in selection to include the initial critical tokens, e.g. sinks. We trained a MoBA variant that always selected the first 16 keys/values for attention in a similar fashion. We found this change alleviated periodic attention sinks, but had negligible effect on downstream performance.
As an aside, though papers such as StreamingLLM have found that softmax attention requires at least one attention sink, there has not been work demonstrating that the frequency of sinks beyond one is necessarily destructive. Furthermore, most works on attention sink focus on relatively short contexts (~256-512), which is too short to observe the transiency of early sinks.
Sparse Attention Key Geometry
We then move to analyze the attention geometry of sparse attention models. We visualize below the t-SNE projection of the query-key manifolds formed from a single long-context rollout across heads/layers.
For MoBA, the centroids lie solidly inside the contextual key manifold. As the keys evolve in time, so do the centroids.
For NSA, the key geometry appears very different due to the heavy grouping factor. Since keys are shared across heads, the key distribution is very isotropic and the burden lies on the head-specific queries to extract contextual information. Hence, we observe the query manifold snaking around the isotropic, centered key cloud in most heads. Due to this isotropy, the centroids are tightly clustered unlike MoBA.
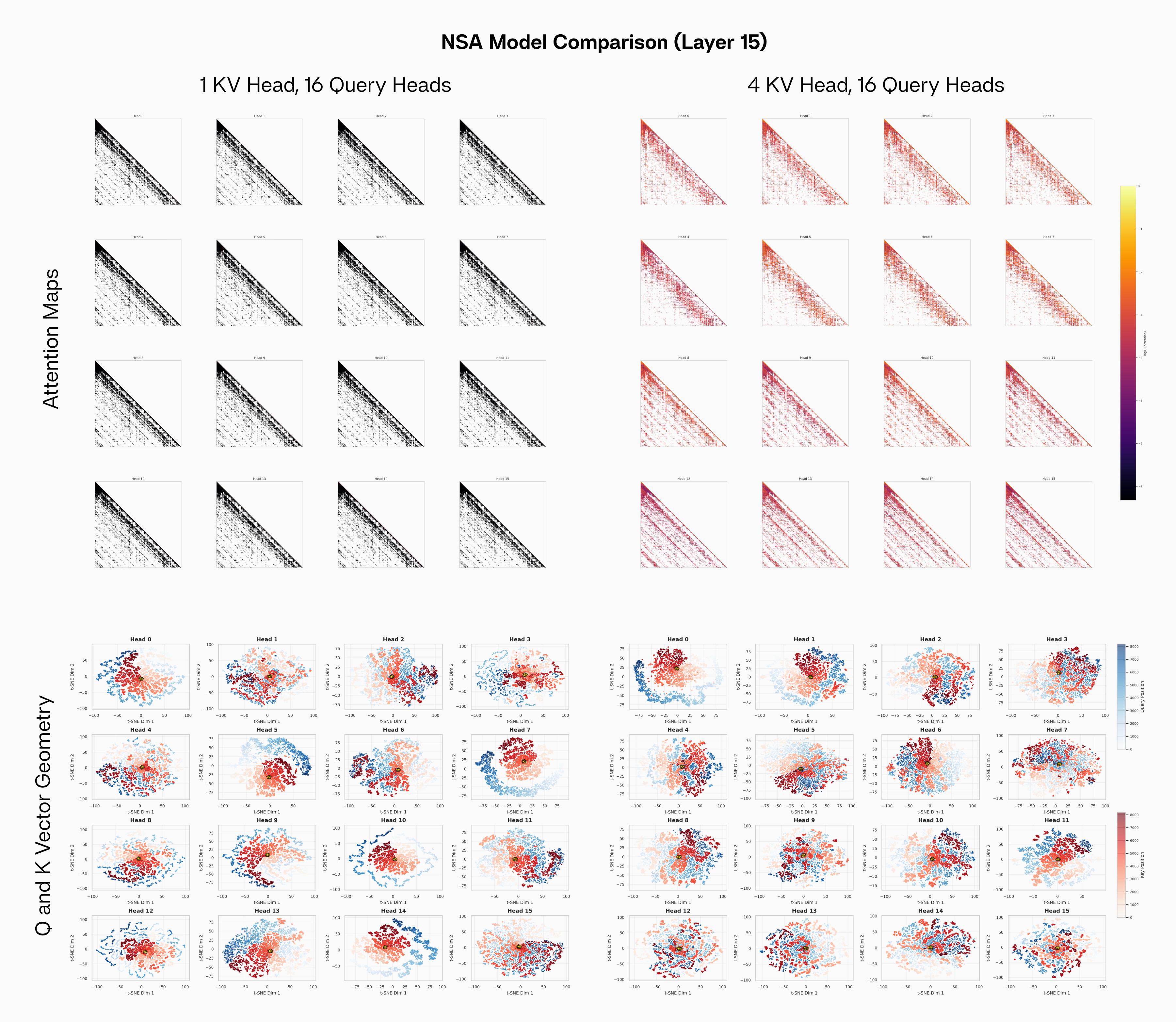 Behavior of NSA attention and key geometry under different GQA constraints (4 vs 1 kv heads).
Behavior of NSA attention and key geometry under different GQA constraints (4 vs 1 kv heads).
NSA models with aggressive GQA have much more sparse attention patterns, even among selected keys, and the key cloud is usually more homogeneoeous. Earlier, we also observed models with aggressive GQA benefitted more strongly from sparse attention.
Taken together, these results suggest a fascinating synergy between GQA and sparse attention. The t-SNE geometry visualization for MQA NSA is particularly indicative of a potential explanation. Under high KV sharing pressure, the key distribution becomes isotropic and the burden falls to the query heads to extract specific parts of the key cloud. We hypothesize that sparse attention reduces interference from other parts of the cloud, enabling diverse head performance. We leave this as a promising direction of future work.
Not all branches are created equal
We analyzed the gating distributions for the NSA model, aggregated across 30 long context examples form the PG 19 dataset. The routing gate outputs the weights per head for each of the three branches - selection, compression, and sliding window. As seen below, the sliding window branch plays a dominant role in later layers, with gate values averaging 0.5. By contrast, the compression branch becomes unutilized after early layers.
We also note strange behavior in the last layer - whereby all three branches are fully active despite compression and selection being inactive in the layers before.
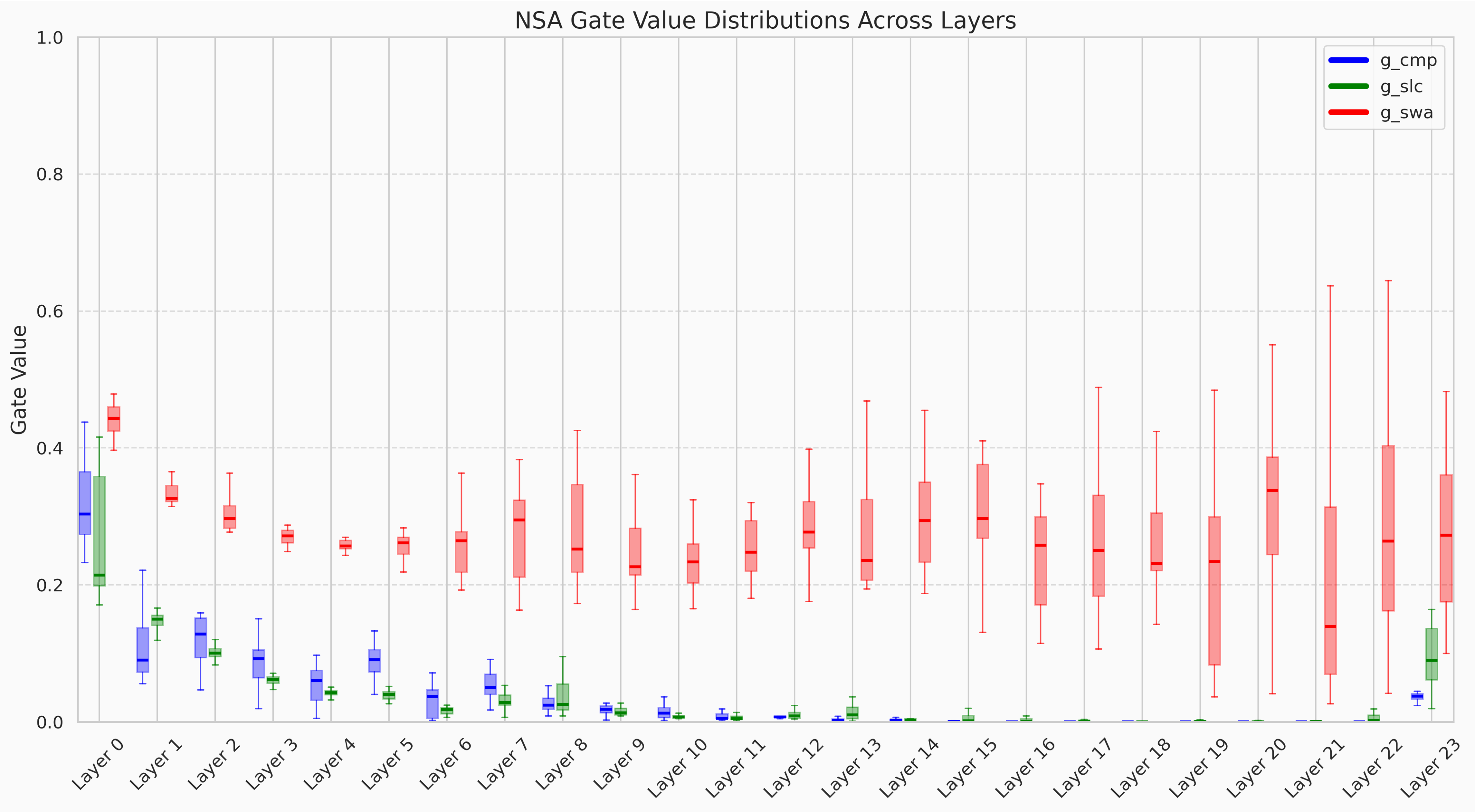 Distributions of gate values for NSA model.
Distributions of gate values for NSA model.
For the NSA MQA model, gate values tend to be correlated across heads. Early in the model, selection and compression branches have consistently high gate correlations across heads. Later in the model, however, selection and sliding window gate values become decorrelated across heads. This suggests that early NSA blocks execute a set of conserved, general purpose induction heads whereas later layers specialize in selecting and retrieving head-specific mixing information.
NSA can be thought of as performing Neural Architecture Search on the attention blocks with three different "architectures" for attention that cooperate and compete at each head (see Appendix B). Our gating analysis reveals that routing decisions for most heads collapse into one or two branches, allowing us to prune away unused branches for certain heads at inference time, dramatically improving throughput. Interestingly, after the first half of the model, sliding window attention dominates the gate values up until the very last layer. These results seem consistent with earlier observations about attention patterns in language models, whereby later layers often implement sparse, local attention and early layers do global mixing [10]. Motivated by our analysis, we replace the later layers with gated sliding window attention only for minimal degradation in performance during inference.
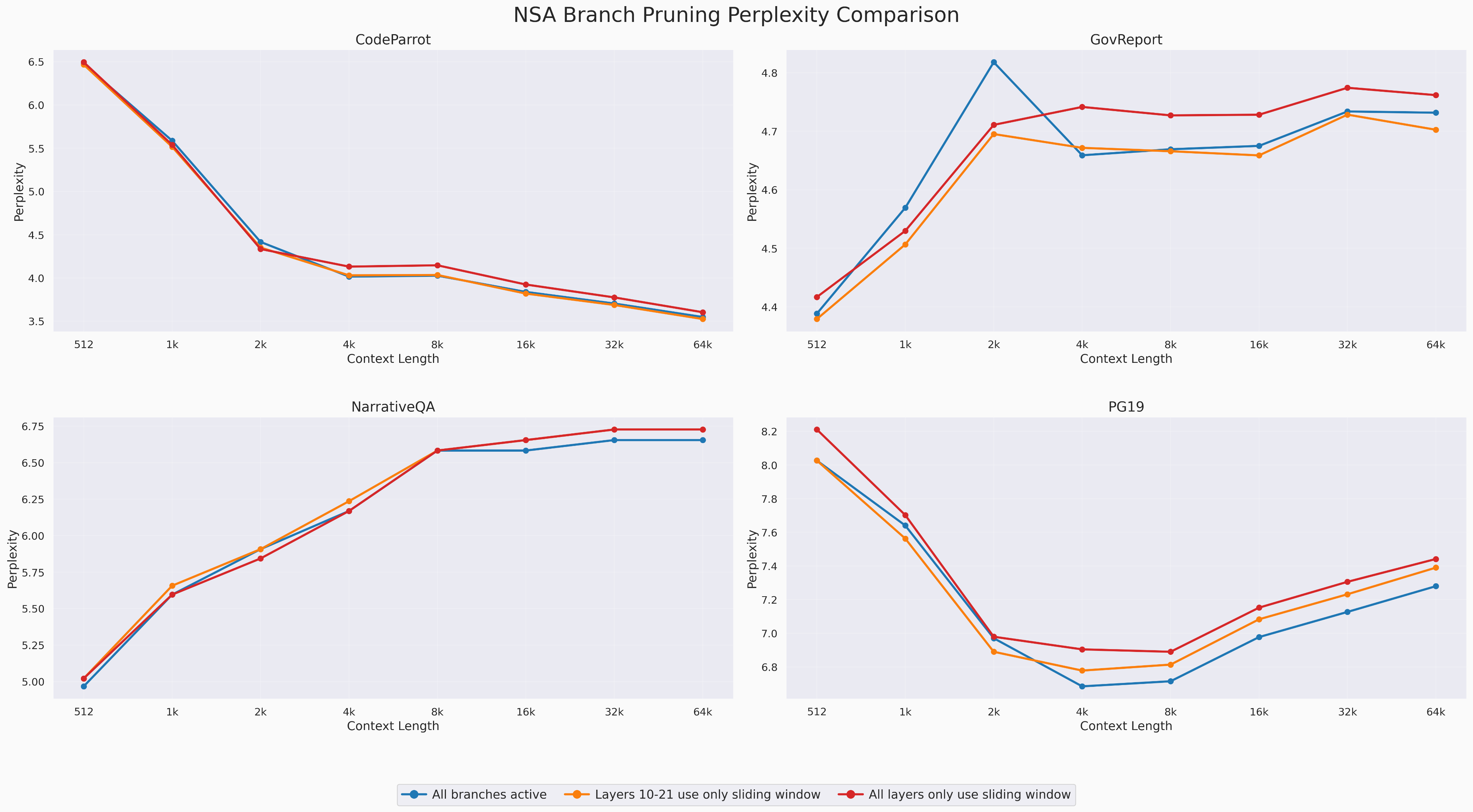 Long context performance after pruning NSA branches. Notably, pruning the later layers based on our earlier analysis actually scores the lowest perplexity on the CodeParrot and GovReport datasets.
Long context performance after pruning NSA branches. Notably, pruning the later layers based on our earlier analysis actually scores the lowest perplexity on the CodeParrot and GovReport datasets.
Selectively ablating layers which do not use compression/selection branches recovers most of the performance of base NSA. Whereas using sliding window only in all layers consistently degrades performance, our principled inference-time intervention recovers most of the gap and boosts throughput for those blocks by 10x at long contexts.
Outlook
As language models continue to evolve, a deep understanding of the mechanisms that enable performance and learning becomes increasingly valuable. We present here a set of preliminary investigations into sparse attention, in the hopes that it will encourage further mechanistic characterization and principled design of architectures.
References
- Ge, Suyu and Zhang, Yunan and Liu, Liyuan and Zhang, Minjia and Han, Jiawei and Gao, Jianfeng (2023).
- Zhang, Zhenyu and Sheng, Ying and Zhou, Tianyi and Chen, Tianlong and Zheng, Lianmin and Cai, Ruisi and Song, Zhao and Tian, Yuandong and Ré, Christopher and Barrett, Clark and others (2023).
- Tang, Jiaming and Zhao, Yilong and Zhu, Kan and Xiao, Guangxuan and Kasikci, Baris and Han, Song (2024).
- Lu, Enzhe and Jiang, Zhejun and Liu, Jingyuan and Du, Yulun and Jiang, Tao and Hong, Chao and Liu, Shaowei and He, Weiran and Yuan, Enming and Wang, Yuzhi and others (2025).
- Yuan, Jingyang and Gao, Huazuo and Dai, Damai and Luo, Junyu and Zhao, Liang and Zhang, Zhengyan and Xie, Zhenda and Wei, YX and Wang, Lean and Xiao, Zhiping and others (2025).
- Liang, Wanchao and Liu, Tianyu and Wright, Less and Constable, Will and Gu, Andrew and Huang, Chien-Chin and Zhang, Iris and Feng, Wei and Huang, Howard and Wang, Junjie and Purandare, Sanket and Nadathur, Gokul and Idreos, Stratos (2025).
- Yang, Songlin and Zhang, Yu (2024).
- Dong, Juechu and Feng, Boyuan and Guessous, Driss and Liang, Yanbo and He, Horace (2024).
- Gu, Xiangming and Pang, Tianyu and Du, Chao and Liu, Qian and Zhang, Fengzhuo and Du, Cunxiao and Wang, Ye and Lin, Min (2025).
- Cai, Zefan and Zhang, Yichi and Gao, Bofei and Liu, Yuliang and Li, Yucheng and Liu, Tianyu and Lu, Keming and Xiong, Wayne and Dong, Yue and Hu, Junjie and Xiao, Wen (2025).
- Yang, An and Li, Anfeng and Yang, Baosong and Zhang, Beichen and Hui, Binyuan and Zheng, Bo and Yu, Bowen and Gao, Chang and Huang, Chengen and Lv, Chenxu et al. (2025).
- Deng, Yichuan and Song, Zhao and Xiong, Jing and Yang, Chiwun (2025).
- Ren, Pengzhen and Xiao, Yun and Chang, Xiaojun and Huang, Po-Yao and Li, Zhihui and Chen, Xiaojiang and Wang, Xin (2021).
Appendix
A. Training Details
All models followed the transformer++ architecture, with RoPE, SwiGLU, pre-LN, etc. We also employ QKV bias and QK-norm (originally scaled in Qwen 3 [11]), after validating that these strategies improved performance. We use an initialization scale of 0.006, the LLaMa/Mistral tokenizer with a vocabulary size of 32k, and a sequence length of 8192. We trained using the AdamW optimizer and a warmup-decay learning rate scheduler. All hyperparameter configurations used sensible baselines.
We use a fixed sparsity ratio for our experiments. For MoBA we set block size to 512 and topk to 3 (as in the original paper), resulting in a maximum of 1536 selected KV entries out of 8192 (81% sparsity). For NSA we set block size to 64, topk to 16, and the sliding window size to 512 to achieve similar sparsity (1536/8192). For simplicity and parameter-efficiency, we use mean pooling NSA as opposed to the MLP used by the authors.
B. Motivating Sparse Attention
In this section we want to offer some brief thoughts on why it is indeed plausible that sparse attention works, and also additional insight into the design choices of NSA.
Above, we mentioned that in practice, attention distributions are highly sparse, and so empirically we might expect that we can "get away with" sparse attention. It turns out that this is justified on theoretical grounds as well: in Deng et. al [12] show that given context length n, if one only considers the largest Ω(n^C) entries, this is enough for sparse attention to approximate (with decreasing loss) the exact attention matrix with, for 0 < C < 1. However, one can perhaps not get away with "too much", as they also show that using too few entries (e.g., ), one incurs large approximation error that increases with context length.
Speculatively, there is also something to be said about whether we even want to be approximating full attention, and instead if we want a mechanism that allows the model to more easily and directly "shut off" certain information. We now say a few words about some intuition for the design choices of each of the NSA branches. We encourage the interested reader to see the NSA paper [5] for more details.
The goal of the compression branch is twofold: to provide higher-level "summaries" of different chunks of the sequence through an approximate attention, and then to do so in a way that reduces the number of attention targets per query, thereby lowering computational cost while preserving global context. The branch pools compressed keys and values block-wise, constructing representative candidates for each contiguous segment in the KV cache. Since the output of this branch is gated and combined in the final output, the scores used in routing enjoy direct supervision from downstream gradients, and there is even upstream gradient flow to the pooling mechanism. This allows NSA to use a parametric pooling mechanism (MLP), as opposed to e.g. the nonparametric mean.
The selection branch then leverages the attention scores from the compression branch to determine which fine-grained blocks to attend to, which makes the selection an adaptive sparse attention strategy. And finally, the sliding window branch is used to ensure the model always maintains local context. Several studies have observed most attention is concentrated on the most recent tokens, and the sliding window branch ensures this information is preserved. The NSA paper also makes the point that having a dedicated branch for this allows the other two branches to not focus on this at all, which is quite interesting.
Compared to other sparse attention mechanisms, e.g. MoBA, NSA is distinguished by its supervision through the pooling/compression through the inclusion of this explicit branch, and its gated combination of the three distinct mechanisms.
NSA is strongly reminiscent of classical Neural Architecture Search (NAS) approaches [13], wherein a supernetwork is constructed which routes between different architectural components with different functional capabilities. A plausible design choice, in light of recent trends in attention alternatives, is to interleave sliding window, compression, and selection blocks separately. However, NSA's approach of ensembling all three mechanisms at each layer allows for much stronger performance and multipurpose functionality of each sequence mixing block - while remaining hardware aligned.